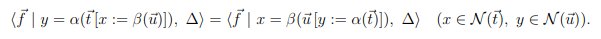Configuration
<... | x = α(...y...), y = β(...x...)>
can be reduced to both
<... | x = α(...β(...x...)...)>
and
<... | y = β(...α(...y...)...)>,
which syntactically appears as a counterexample to strong confluence, while essentially representing the same configuration.
Is there a way to formalize equivalence between those two normal forms?
I think there is:
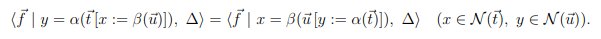
<... | x = α(...y...), y = β(...x...)>
can be reduced to both
<... | x = α(...β(...x...)...)>
and
<... | y = β(...α(...y...)...)>,
which syntactically appears as a counterexample to strong confluence, while essentially representing the same configuration.
Is there a way to formalize equivalence between those two normal forms?
I think there is: