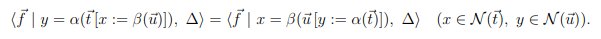После конференции TERMGRAPH в Эйндховене понял, что хорошо было бы иметь под рукой готовое быстрое введение одновременно в сети взаимодействия и исчисление взаимодействия. Вот что получилось из этой идеи.Сети взаимодействия (interaction nets) - это структуры, подобные графам, состоящие из
агентов (agents) и дуг. Агент типа α
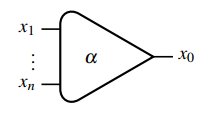
имеет арность ar(α) ≥ 0. Если ar(α) = n, то агент α имеет n
дополнительных портов (auxiliary ports) x
1,..., x
n в дополнение к его
главному порту (principle port) x
0. Все типы агентов принадлежат множеству Σ, называемому
сигнатурой (signature). К любому порту можно присоединить не более одной дуги. Порты, которые не соединены ни одной дугой, называются
свободными (free ports). Совокупность всех свободных портов в сети называется ее
интерфейсом.
Разводка (wiring) ω

состоит исключительно из дуг. Индуктивно определяемые
деревья (trees)

соответствуют
термам t
::= α(t
1,..., t
n) | x в исчислении взаимодействия (interaction calculus), где x называется
именем (name).
С помощью разводок и деревьев любая сеть может быть представлена следующим образом:

что в исчислении взаимодействия будет соответствовать
конфигурации (configuration)
<t
1,..., t
m | v
1 = w
1,..., v
n = w
n>,
где t
i, v
i, w
i - некоторые термы. Последовательность t
1,..., t
m называется
интерфейсом (interface), остальное же представляет собой мультимножество
уравнений (equations). Разводка ω транслируется в выбор имен, и каждое имя обязано иметь ровно два вхождения в конфигурации.
Как и в λ-исчислении, в исчислении взаимодействия естественным образом определяются понятия α-конверсии и подстановки (substitution). Оба вхождения любого имени могут быть заменены на новое имя, если оно не участвует в данной конфигурации. Если терм t имеет ровно одно вхождение имени x, то
подстановка t[x := u] определяется как результат замены имени x в терме t некоторым термом u.
Когда два агента соединены своими главными портами, они формируют
активную пару (active pair). Для активных пар можно ввести
правила взаимодействия (interaction rules), которые описывают, как активная пара будет заменена во время редукции сети взаимодействия. Графически любое правило взаимодействия можно преставить следующим образом:

где α, β ∈ Σ, а сеть N представлена с помощью разводок и деревьев в виде, пригодном для исчисления взаимодействия: в нотации Lafont это соответствует
a[v
1,..., v
m] >< β[w
1,..., w
n].
Говорят, что сеть без активных пар находится в
нормальной форме (normal form). Сигнатура и множество правил взаимодействия вместе задают
систему взаимодействия (interaction system).
Теперь рассмотрим пример для введенных конструкций, в котором участвуют часто использующиеся агенты ε и δ. В нотации Lafont правила взаимодействия для удаляющего (erasing) агента ε

записываются как ε >< α[ε,..., ε], а правила для дублирующего (duplicating) агента δ

выглядят следующим образом:
δ[α(x
1,..., x
n), α(y
1,..., y
n)] >< α[δ(x
1, y
1),..., δ(x
n, y
n)].
В качестве примера сети, в которой участвуют правила удаления и дублирования, возьмем простую сеть которая не имеет нормальной формы и редуцируется к самой себе:

В исчислении взаимодействия такая сеть соответствует конфигурации
<∅ | δ(ε, x) = γ(x, ε)> без интерфейса.
Редукция для конфигураций определяется более подробно, чем для сетей. Если
a[v
1,..., v
m] >< β[w
1,..., w
n], то следующая редукция:
<... | α(t
1,..., t
m) = β(u
1,..., u
n), Δ> → <... | t
1 = v
1,..., t
m = v
m, u
1 = w
1,..., u
n = w
n, Δ>
называется
взаимодействием (interaction). Когда одно из уравнений имеет форму x = u, к конфигурации применимо
разыменование (indirection), в результате которого другое вхождение имени x в некотором терме t будет заменено на терм u:
<...t... | x = u, Δ> → <...t[x := u]... | Δ> или <... | x = u, t = w, Δ> → <... | t[x := u] = w, Δ>.
Уравнение t = x называется
тупиком (deadlock), если x имеет вхождение в t. Обычно рассматривают только сети, свободные от тупиков (deadlock-free). Вместе взаимодействие и разыменование задают отношение редукции на конфигурациях. Тот факт, что некоторая конфигурация c редуцируется к своей
нормальной форме c', где мультимножество уравнений пусто, обозначают через c ↓ c'.
Если вернуться к примеру незавершающейся редукции сети, то бесконечная редукционная цепочка, начинающаяся с соответствующей конфигурации выглядит следующим образом:
<∅ | δ(ε, x) = γ(x, ε)> →
<∅ | ε = γ(x
1, x
2), x = γ(y
1, y
2), x = δ(x
1, y
1), ε = δ(x
2, y
2)> →
*<∅ | x
1 = ε, x
2 = ε, x = γ(y
1, y
2), x = δ(x
1, y
1), x
2 = ε, y
2 = ε> →
*<∅ | δ(ε, x) = γ(x, ε)> → ...
На нашем языке программирования, который подобен yacc(1)/lex(1) по структуре и лексически близок к LaTeX-нотации для исчисления взаимодействия, тот же самый пример можно записать следующим образом:
\epsilon {
console.log("epsilon >< delta");
} \delta[\epsilon, \epsilon];
\epsilon {
console.log("epsilon >< gamma");
} \gamma[\epsilon, \epsilon];
\delta[\gamma(x, y), \gamma(v, w)] {
console.log("delta >< gamma");
} \gamma[\delta(x, v), \delta(y, w)];
$$
\delta(\epsilon, x) = \gamma(x, \epsilon);Отметим, что наш язык программирования позволяет записывать побочные действия в императивном стиле, таким образом давая возможность исполнять произвольный код, включая ввод-вывод, а также условные множественные правила для пар вида α
i >< β
j в зависимости от значений i и j, которые могут быть произвольными данными, привязанными к агентам.
Наша реализация этого языка программирования не полагается какую-либо внешнюю сборку мусора, так как не занимается контролем связности сети. Данное свойство является следствием того, что интерфейс сети предполагается пустым, а сети задаются исключительно через мультимножества уравнений. Чтобы записать в нашем языке некоторую сеть с непустым интерфейсом, необходимо сначала ее модифицировать, например, добавив агенты с нулевой арностью ко всем свободным портам.
Сигнатура и арности агентов соответствующей системы взаимодействия автоматически выводятся при компиляции исходного кода программы на основе правил взаимодействия и начальной конфигурации. Правила взаимодействия вместе с их побочными действиями компилируются заранее, до начала редукции сети, при этом компилятор формирует таблицу для быстрого O(1)-поиска правил, соответствующих активным парам, во время последующего исполнения программы. После этого начальная конфигурация добавляется в FIFO-очередь уравнений, которая затем обрабатывается, пока она не станет пуста.
P. S. Недавно адаптировал этот текст и дополнил им статью на Википедии.