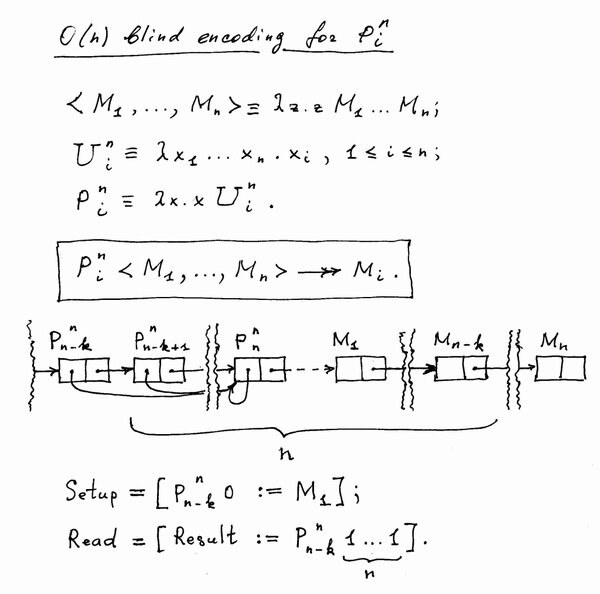codedot | Entries tagged with lambda calculus

Килобит можно передать одним сообщением по SMS.

При этом его достаточно, чтобы адресовать любую точку пространства-времени с точностью до планковских единиц измерения на протяжении 10²⁷ лет, что в 10¹⁷ раз больше, чем уже прошло после момента Большого взрыва. Для сравнения, полкилобита адресуют около ста микросекунд. Для данной оценки использовался гиперобъем гиперконуса, который примерно равен гиперобъему гиперкуба со стороной, равной высоте этого гиперконуса.

Таким образом, килобитных адресов хватает на любую мыслимую на сегодняшний день научную фантастику: с невероятным запасом покрываются нужды однозначной адресации для реализованных и доведенных до совершенства квантового компьютера, телепортации, машины времени и кротовых нор вместе взятых.

Теперь предположим, что у нас есть хэш-функция F, похожая на SHA-2, но с размером хэша и размером блока ровно в один килобит (вместо обычных 256 бит и 512-битных блоков), и способ адресации, подобный .onion-доменам для анонимных сервисов в сети Tor, причем каждый сервис хранит ровно одну килобитную ячейку памяти.

Интересно было бы рассмотреть распределенную RAM0-подобную вычислительную сеть с семантикой команд, измененной следующим образом (предполагается отсутствие коллизиций на килобитных блоках):

#define A	z = F(z)
#define L	z = recvkbit(z)
#define N	n = z
#define S	sendkbit(n, z)

Программы на языке MLC (Macro Lambda Calculus) - пример доступен на GitHub - имеют следующий вид:

N1 = M1;
...
Nm = Mm;

M0.

Выражение M0 может содержать произвольное число вхождений имен макросов N1, ... , Nm, а также свободных переменных - обозначим их x1, ... , xn. Комбинатор M, нормальную форму которого мы фактически ищем, получается из программы следующим образом:

M = x1, ... , xn: (N1, ... , Nm: M0) M1 ... Mm.

Комбинатор M, в свою очередь, представим в исчислении взаимодействия, воспользовавшись направленной версией компактной кодировки λ-выражений. Заметим, что конфигурация <x | Γ(M, x)>, как можно видеть из определения, содержит только редексы по левому разыменованию. Следовательно, чтобы инициализировать нашу систему слепой перезаписи графов, достаточно все уравнения конфигурации положить в стек, соответствующий левому разыменованию.

Полученную в результате структуру памяти можно восстановить некоторой последовательностью I инструкций Z, A, L, N и S машины RAM0. Основной цикл работы нашей системы слепой перезаписи графов, реализующей редукцию сетей взаимодействия, также может быть представлен некоторой последовательностью R инструкций Z, A, L, N и S, которая не зависит от вычисляемого выражения. Таким образом, исходный код на языке MLC может быть скомпилирован в следующую программу RAM0:

I;
loop: R;
goto loop;

Данная программа не содержит инструкцию C для условного перехода. Такие детали, как стратегия вычисления, остановка машины, обработка дна стеков и механизм "read-back" во время стягивания конфигурации, были здесь намеренно опущены, чтобы не нагромождать и без того уже объемное изложение.

Модель RAM0 (Schönhage's zero-parameter successor RAM model) - это компьютер с двумя регистрами (z и n) и шестью командами (Z, A, L, N, S и C), который эквивалентен SMM (Schönhage's storage modification machine model).

Как следует из названия, команды RAM0, за исключением, пожалуй, условного перехода, не имеют параметров. Одна из ее особенностей - алгоритм умножения n-битных чисел за линейное время O(n). Этот, на первый взгляд, парадоксальный результат говорит о том, что механизм RAM сам по себе обладает определенной вычислительной мощностью.

На языке Си команды RAM0 выглядят следующим образом:

#ifndef _RAM0_H
#define _RAM0_H

#include <stdlib.h>

extern void **n, **z;

#define Z	z = NULL
#define A	++z
#define L	z = *z
#define N	n = z
#define S	*n = z

#define C(label) \
	do { \
		if (z) \
			goto label; \
	} while (0)

#endif

Ниже пример программы:

#include "ram0.h"

void **n, **z;

main()
{
	loop: Z; A; L; N; S; C(loop);

	return !z;
}

Интересно, что система сохраняет Тьюринг-полноту, даже если заменить условный переход безусловным. Эта задача рассматривается в статьях "Blind graph rewriting systems" и "A compact encoding for λ-terms in interaction calculus".

http://mathoverflow.net/questions/129923

It is possible to implement λ-calculus in Schönhage's storage modification machine using an infinite set of nodes and one single program consisted exclusively of (about hundred) instructions set w to v (with different w and v) using a compact directed encoding for λ-terms closely related to directed interaction combinators by Lafont, and four infinite spaghetti stacks based on linked nodes to perform interaction and indirection rules on configurations.

Is it possible to preserve Turing-completeness of the SMM model while restricting its instruction set to only a single instruction set w to v (with constant w and v) during the whole computation process?

I would be very grateful for any references regarding this question.

In theoretical computer science a pointer machine is an "atomistic" abstract computational machine model akin to the Random access machine.

Depending on the type, a pointer machine may be called a linking automaton, a KU-machine, an SMM, an atomistic LISP machine, a tree-pointer machine, etc. (cf Ben-Amram 1995). At least three major varieties exist in the literature—the Kolmogorov-Uspenskii model (KUM, KU-machine), the Knuth linking automaton, and the Schönhage Storage Modification Machine model (SMM). The SMM seems to be the most common.

This should definitely help to answer two questions on MathOverflow, regarding Turing-complete primitive blind automata and Universality of blind graph rewriting.

IBM Journal of Research and Development, vol. 5, pp. 183-191 (1961)
Rolf Landauer

It is argued that computing machines inevitably involve devices which perform logical functions that do not have a single-valued inverse. This logical irreversibility is associated with physical irreversibility and requires a minimal heat generation, per machine cycle, typically of the order of kT for each irreversible function. This dissipation serves the purpose of standardizing signals and making them independent of their exact logical history. Two simple, but representative, models of bistable devices are subjected to a more detailed analysis of switching kinetics to yield the relationship between speed and energy dissipation, and to estimate the effects of errors induced by thermal fluctuations.

http://folk.uio.no/feder/Fys3130/Entropy/Landauer1961.pdf

See also discussion of Landauer's principle.

В монографии "Ламбда-исчисление. Его синтаксис и семантика", Барендрегт Х., 1985 (перевод с английского Г. Е. Минца под редакцией А. С. Кузичева), в параграфе 16.4 рассматривается эквациональная теория B = {M = N | M, N ∈ Λ₀, BT(M) = BT(N)}, где BT(M) - дерево Бема для терма M (см. "Краткое изложение λ-исчисления"). Иными словами, в этой теории отождествяются термы, имеющие одни и те же деревья Бема. Теория B непротиворечива, так как является собственным подмножеством ее экстенсионального расширения Bη, которое, в свою очередь, совпадает с единственной HP-полной λ-теорией H*.

Все комбинаторы неподвижной точки имеют одно и то же дерево Бема, поэтому они отождествляются в теории B. Более того, существуют термы, которые формально не подпадают под определение комбинаторов неподвижной точки, но имеют то же самое дерево Бема. Термы, которым соответствует дерево Бема комбинаторов неподвижной точки, обобщенно называются нестандартными комбинаторами неподвижной точки, а термы из этого множества, не являющиеся комбинаторами неподвижной точки, в свою очередь, называют существенно нестандартными. В следующей статье показывается, что множество нестандартных комбинаторов неподвижной точки не является рекурсивно перечислимым, в отличие от множества обычных комбинаторов неподвижной точки.

On the Recursive Enumerability of Fixed-Point Combinators
Mayer Goldberg

We show that the set of fixed-point combinators forms a recursively-enumerable subset of a larger set of terms we call non-standard fixed-point combinators. These terms are observationally equivalent to fixed-point combinators in any computable context, but the set of non-standard fixed-point combinators is not recursively enumerable.

http://www.brics.dk/RS/05/1/BRICS-RS-05-1.pdf

Operational equivalence for interaction nets
Maribel Fernández, Ian Mackie

The notion of contextual (or operational) equivalence is fundamental in the theory of programming languages. By setting up a notion of bisimilarity, and showing that it coincides with contextual equivalence, one obtains a simple coinductive proof technique for showing that two programs are equivalent in all contexts. In this paper we apply these (now standard) techniques to interactions nets, a graphical programming language characterized by local reduction. This work generalizes previous studies of operational equivalence in typed interaction nets since it can be applied to untyped systems, thus all systems of interaction nets are captured.

http://www.sciencedirect.com/science/article/pii/S0304397502006370

Observational Equivalence for the Interaction Combinators and Internal Separation
Damiano Mazza

We define an observational equivalence for Lafont's interaction combinators, which we prove to be the least discriminating non-trivial congruence on total nets (nets admitting a deadlock-free normal form) respecting reduction. More interestingly, this equivalence enjoys an internal separation property similar to that of Böhm's Theorem for the λ-calculus.

http://www.sciencedirect.com/science/article/pii/S1571066107001880

http://mathoverflow.net/questions/126941/

Существуют несколько способов представить λ-термы в сетях взаимодействия; например, алгоритм Лэмпинга для оптимальной редукции или компиляция λ-исчисления в комбинаторы взаимодействия. Однако, все известные нам способы реализуют только β-редукцию, но не экстенсиональное λ-исчисление (где также есть η-редукция).

Можно ли представить λ-термы в сетях взаимодействия, реализовав βη-редукцию?

(Нормальная форма сети для терма должна соответствовать его βη-нормальной форме.)

http://arxiv.org/abs/1304.1309

Interaction Nets in Russian

Draft translation to Russian of Chapter 7, Interaction-Based Models of Computation, from Models of Computation: An Introduction to Computability Theory by Maribel Fernandez. "In this chapter, we study interaction nets, a model of computation that can be seen as a representative of a class of models based on the notion of 'computation as interaction'. Interaction nets are a graphical model of computation devised by Yves Lafont in 1990 as a generalisation of the proof structures of linear logic. It can be seen as an abstract formalism, used to define algorithms and analyse their cost, or as a low-level language into which other programming languages can be compiled. This is fruitful because interaction nets can be implemented with reasonable efficiency."

Andrej Bauer
University of Ljubljana, Slovenia; Member, School of Mathematics
March 18, 2013 - 2:00pm

Discussions about constructive mathematics are usually derailed by philosophical opinions and meta-mathematics. But how does it actually feel to do constructive mathematics? A famous mathematician wrote that "taking the principle of excluded middle from the mathematician would be the same, say, as proscribing the telescope to the astronomer or to the boxer the use of his fists." Was he right? In this talk we shall visit the astounding worlds of constructive mathematics. As tourists from the classical world we will at first be shocked by the bizarre and unfamiliar phenomena, but hopefully also left curious about the new possibilities and dimensions of mathematics that the classical dogma declares heretical or even non-existent.

http://video.ias.edu/members/1213/0318-AndrejBauer

Я перевел на русский язык седьмую главу "Interaction-Based Models of Computation" из учебника "Models of Computation: An Introduction to Computability Theory" (Maribel Fernández). Исходник и PDF доступны на ShareLaTeX по следующему адресу:

https://www.sharelatex.com/project/515429c83d69291740451afe

В этой главе изучаются сети взаимодействия - модель вычислений, которую можно рассматривать как представителя класса моделей, основанных на идее "вычислений через взаимодействие". Сети взаимодействия являются графической моделью вычислений, изначально введенной как обобщение структур доказательств линейной логики. Данный формализм используется для описания алгоритмов и анализа их сложности, а также как язык низкого уровня, в который можно компилировать другие языки программирования. Особенно интересны сети взаимодействия тем, что они могут быть реализованы с разумной эффективностью.

Системы сетей взаимодействия определяются двумя множествами: набором агентов и набором правил взаимодействия. Агенты играют роль логических символов, а правила взаимодействия определяют их смысл. Также возможна аналогия с электрическими цепями, где агенты играют роль узлов цепи, а связи между агентами служат ветвями, соединяющими узлы. Наконец, мы можем просто считать агенты некоторыми объектами, выполняющими вычисления, при этом правила взаимодействия описывают их поведение.

Здесь дается общее представление о парадигме взаимодействия, приводятся примеры использования сетей взаимодействия для представления алгоритмов, а также показывается, как другие модели вычислений представляются в виде сетей взаимодействия.

http://arxiv.org/abs/1304.0558

This text gives a rough, but linear summary covering some key definitions, notations, and propositions from Lambda Calculus: Its Syntax and Semantics, the classical monograph by Barendregt. First, we define a theory of untyped extensional lambda calculus. Then, some syntactic sugar, a system of combinatory logic, and the fixed point theorem are described. The final section introduces a topology on the set of lambda terms which is meant to explain an illusory contradiction. Namely, functions defined on the set of lambda terms are in the set of lambda terms itself, the latter being a countable set. However, the functions on the set of lambda terms appear to be continuous with respect to a topology of trees.

На ShareLaTeX теперь доступно краткое изложение λ-исчисления:

https://www.sharelatex.com/project/5154436b3d6929174048f846

Данный текст представляет собой чрезвычайно сжатый конспект классической монографии по λ-исчислению (Х. Барендрегт, «Ламбда-исчисление. Его синтаксис и семантика», перевод с английского Г. Е. Минца под редакцией А. С. Кузичева, Москва, «Мир», 1985).

Он может оказаться интересен всем тем, кто планировал взяться за систематическое изучение данной темы, уже в общих чертах ознакомившись с ней, но откладывал из-за сложной структуры основной монографии, определения и основные результаты в которой довольно разрозненны. Здесь мы попытаемся сделать изложение, напротив, абсолютно линейным, и, конечно, несравнимо более коротким, избегая лишних определений и примеров, а сосредоточившись на необходимых терминологии, обозначениях и утверждениях, которые, в свою очередь, изложены близко к оригинальному тексту.

Мы начнем от определения системы λβη, то есть классического бестипового экстенсионального λ-исчисления. Затем перейдем к комбинаторной логике, теореме о неподвижной точке и синтаксическому сахару. Наконец, заключительная часть конспекта — построение топологии на выражениях этой системы, призванной объяснить кажущееся противоречие: отображения множества выражений в себя содержатся в самом этом множестве при его счетности. На самом же деле, множество наделяется надлежащей топологией, в которой выражения представляют собой непрерывные отображения.

Кстати, сервис ShareLaTeX оказался чрезвычайно удобным. Горячо рекомендую его для хранения математических текстов и, в том числе совместного, их редактирования. Собираюсь использовать его для перевода седьмой главы о системах взаимодействия прекрасного учебника по моделям вычислений. Скорее всего, перевод будет доступен по следующему адресу:

https://www.sharelatex.com/project/515429c83d69291740451afe

Всячески рекомендую всем замечательный учебник Maribel Fernandez под названием "Models of Computation: An Introduction to Computability Theory". С одной стороны, он написан сжато и по существу, но при этом простым языком, содержит упражнения и покрывает современный материал.

Учебник начинается с введения в классическую теории вычислимости: машины Тьюринга и лямбда-исчисление. Затем следует подробное описание систем взаимодействия, включая полезную нотацию Lafont. Наконец, дается обзор некоторых зарождающихся направлений.

A Concise Introduction to Computation Models and Computability Theory provides an introduction to the essential concepts in computability, using several models of computation, from the standard Turing Machines and Recursive Functions, to the modern computation models inspired by quantum physics. An in-depth analysis of the basic concepts underlying each model of computation is provided. Divided into two parts, the first highlights the traditional computation models used in the first studies on computability:

- Automata and Turing Machines;
- Recursive functions and the Lambda-Calculus;
- Logic-based computation models.

The second part covers object-oriented and interaction-based models. There is also a chapter on concurrency, and a final chapter on emergent computation models inspired by quantum mechanics. At the end of each chapter there is a discussion on the use of computation models in the design of programming languages.

http://www.amazon.co.uk/dp/1848824335

Мы уже затрагивали переход от условного выражения к функциям-проекциям для конечных последовательностей, когда обсуждали логические операции без сравнений. Однако, теперь мы можем обобщить также условное выражение, реализованное с помощью одной примитивной операции, а не двух, как раньше. Мы будем опираться на определения и обозначения, введенные при рассмотрении GRS из одной примитивной операции.

Благодаря незамысловатому разделению памяти, для представления всех функций-проекций для последовательностей длиной n или менее элементов, нам потребуется ровно n нод:

Заметим, что условное выражение B M N "если B, то M, иначе N", где "истина" T = λxy.x и "ложь" F = λxy.y, является частным случаем конструкций выше.

kolbusa @ 2013-02-22 18:43:00:

x86 MMU fault handling is Turing complete:

http://news.ycombinator.com/item?id=5261598

http://www.youtube.com/watch?v=Y1ypnYIyzKk

IEEE 1003.1-2008, C.4.3 Exclusion of Utilities:

emacs

The community of emacs editing enthusiasts was adamant that the full emacs editor not be included in the base documents because they were concerned that an attempt to standardize this very powerful environment would encourage vendors to ship versions conforming strictly to the standard, but lacking the extensibility required by the community. The author of the original emacs program also expressed his desire to omit the program. Furthermore, there were a number of historical UNIX systems that did not include emacs, or included it without supporting it, but there were very few that did not include and support vi.

Напомним, что подпроект inet (см. "Анонс нового языка программирования", "Интерфейс к симуляторам систем взаимодействия" и "Пример работы симулятора системы взаимодействия") был предназначен, прежде всего, для декодирования и печати результатов работы нашей слепой системы (см. "Взаимодействие с эффектами"). А именно, мы построили специальную систему взаимодействия для выполнения "readback", наделив ее правила побочными действиями:

Σ = {(ε, 0), (γ, 2), (ψ, 2), (c, 1), (@_l, 2), (@_r, 2)} ∪ {(x_i, 0) | i ∈ N} ∪ {(λ_i, 1) | i ∈ N};

λ_i[λ_i(ε)] >< x_j + "x_j";
λ_i[a] >< γ[λ_{i + 1}(c(a)), x_i] + "(λx_i.";
x_i >< ψ[x_i, x_i];
x_i >< γ[a, @_l(x_i, a)];
λ[a] >< @_l[λ(@_r(b, a)), b] + "(";
λ[a] >< c[λ(a)] + ")";
λ[ε] >< @_r[λ(c(a)), a] + " ".

Теперь же для подобных систем у нас есть специальный язык программирования и компилятор для него. С его помощью мы добавили readback-модуль в наш интерпретатор MLC незамысловатым изменением (слепую систему мы будем заставлять работать только по мере того, как автоматически сгененрированный readback-модуль будет вызывать функцию inaux() против недостающих частей вычисляемого выражения):

diff --git a/Makefile b/Makefile
index 3c480f1..32a7b9c 100644
--- a/Makefile
+++ b/Makefile
@@ -1,5 +1,6 @@
 CFLAGS = -Iblind
 YFLAGS = -dv
+INC = inet/inc
 
 OBJS = \
 	eval.o \
@@ -10,6 +11,7 @@ OBJS = \
 	new.o \
 	parser.o \
 	prepare.o \
+	readback.o \
 	show.o
 
 all: subdir example.mlc
@@ -34,6 +36,13 @@ lexer.o: parser.o
 $(OBJS): human.h
 
 clean:
-	-rm -fr mlc y.* *.o lib.a
+	-rm -fr mlc in.* y.* *.o lib.a
 	cd blind && $(MAKE) clean
 	cd inet && $(MAKE) clean
+
+.SUFFIXES: .in
+
+.in.o:
+	$(INC) <$<
+	$(CC) $(CFLAGS) -c in.tab.c
+	mv in.tab.o $@
diff --git a/readback.in b/readback.in
new file mode 100644
index 0000000..04e7419
--- /dev/null
+++ b/readback.in
@@ -0,0 +1,31 @@
+${
+#include <stdio.h>
+}$
+
+\lambda_{i}[\lambda_{i}(\epsilon)] {
+	printf("x%d", j);
+} \x_{j};
+
+\lambda_{i}[a] {
+	printf("(x%d: ", i);
+} \gamma[\lambda_{i + 1}(\c(a)), \x_{i}];
+
+\x_{i} {
+	/* Unsharing. */
+} \psi[\x_{i}, \x_{i}];
+
+\x_{i} {
+	/* Application. */
+} \gamma[a, \appl(\x_{i}, a)];
+
+\abstr[a] {
+	putchar('(');
+} \appl[\abstr(\appr(b, a)), b];
+
+\abstr[a] {
+	putchar(')');
+} \c[\abstr(a)];
+
+\abstr[\epsilon] {
+	putchar(' ');
+} \appr[\abstr(\c(a)), a].

Отныне inet планируется поддерживать в репозитарии MLC, но прежний репозитарий пока останется для истории. Рецензия кода inet, его дополнительное тестирование и предложения по улучшению работы компилятора, а также интерфейса к нему всячески приветствуются.

https://github.com/euromake/mlc/tree/master/inet

Месяц назад мы анонсировали новый язык программирования. Чуть позже мы подготовили проектную документацию. Теперь же мы реализовали компилятор этого языка программирования. Ниже пример работы тестового приложения, которое задействует симулятор простой системы взаимодействия, автоматически сгенерированный из ее описания.

alexo@euromake:~/inet$ make
./inc <example.in
cc  -c in.tab.c
mv in.tab.o example.o
cc     test.c example.o   -o test
./test
fan_1 >< fan_2
inaux: rewires
inaux: returns
inaux: returns
inaux: returns
inaux: returns
erase >< fan_3
erase >< fan_3
erase >< erase
fan_3 >< fan_3
erase >< erase
alexo@euromake:~/inet$

Profile

Anton Salikhmetov

November 2018

S	M	T	W	T	F	S
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

Syndicate

Page Summary

Tor-подобная килобитная RAM0
Компиляция из MLC в RAM0
RAM0
Schönhage’s SMM with only one instruction
Schönhage's Storage Modification Machine
Irreversibility and heat generation in the computing process
Нестандартные комбинаторы неподвижной точки
Bisimilarity vs. Observational Equivalence
η-редукция в сетях взаимодействия
Draft Russian Translation: Interaction-Based Models of Computation
Five Stages of Accepting Constructive Mathematics
"Interaction Nets" по-русски
Lambda Calculus Synopsis
Краткое изложение λ-исчисления
Прекрасный учебник по моделям вычислений
P^n_i из одной примитивной операции
Turing-complete x86 MMU Page Fault Handling
Emacs
Readback-модуль MLC
Пример работы симулятора системы взаимодействия

Style Credit

Style: Plain for Tabula Rasa

Expand Cut Tags

No cut tags

Page generated Aug. 14th, 2025 07:20 pm