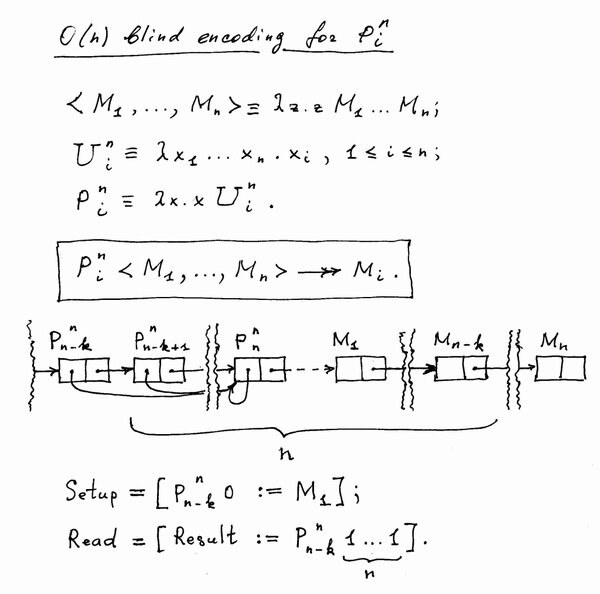codedot | Recent Entries

Модель RAM0 (Schönhage's zero-parameter successor RAM model) - это компьютер с двумя регистрами (z и n) и шестью командами (Z, A, L, N, S и C), который эквивалентен SMM (Schönhage's storage modification machine model).

Как следует из названия, команды RAM0, за исключением, пожалуй, условного перехода, не имеют параметров. Одна из ее особенностей - алгоритм умножения n-битных чисел за линейное время O(n). Этот, на первый взгляд, парадоксальный результат говорит о том, что механизм RAM сам по себе обладает определенной вычислительной мощностью.

На языке Си команды RAM0 выглядят следующим образом:

#ifndef _RAM0_H
#define _RAM0_H

#include <stdlib.h>

extern void **n, **z;

#define Z	z = NULL
#define A	++z
#define L	z = *z
#define N	n = z
#define S	*n = z

#define C(label) \
	do { \
		if (z) \
			goto label; \
	} while (0)

#endif

Ниже пример программы:

#include "ram0.h"

void **n, **z;

main()
{
	loop: Z; A; L; N; S; C(loop);

	return !z;
}

Интересно, что система сохраняет Тьюринг-полноту, даже если заменить условный переход безусловным. Эта задача рассматривается в статьях "Blind graph rewriting systems" и "A compact encoding for λ-terms in interaction calculus".

http://mathoverflow.net/questions/129923

It is possible to implement λ-calculus in Schönhage's storage modification machine using an infinite set of nodes and one single program consisted exclusively of (about hundred) instructions set w to v (with different w and v) using a compact directed encoding for λ-terms closely related to directed interaction combinators by Lafont, and four infinite spaghetti stacks based on linked nodes to perform interaction and indirection rules on configurations.

Is it possible to preserve Turing-completeness of the SMM model while restricting its instruction set to only a single instruction set w to v (with constant w and v) during the whole computation process?

I would be very grateful for any references regarding this question.

In theoretical computer science a pointer machine is an "atomistic" abstract computational machine model akin to the Random access machine.

Depending on the type, a pointer machine may be called a linking automaton, a KU-machine, an SMM, an atomistic LISP machine, a tree-pointer machine, etc. (cf Ben-Amram 1995). At least three major varieties exist in the literature—the Kolmogorov-Uspenskii model (KUM, KU-machine), the Knuth linking automaton, and the Schönhage Storage Modification Machine model (SMM). The SMM seems to be the most common.

This should definitely help to answer two questions on MathOverflow, regarding Turing-complete primitive blind automata and Universality of blind graph rewriting.

root@debian:~# apt-get install tor
Reading package lists... Done
Building dependency tree       
Reading state information... Done
[...]
root@debian:~# grep '^Hidden' /etc/tor/torrc
HiddenServiceDir /var/lib/tor/honey/
HiddenServicePort 22 127.0.0.1:22
root@debian:~# /etc/init.d/tor restart
Stopping tor daemon: tor.
Raising maximum number of filedescriptors (ulimit -n) to 8192.
Starting tor daemon: tor...
[...]
May 03 20:08:30.201 [notice] Opening Socks listener on 127.0.0.1:9050
done.
root@debian:~# torsocks ssh `cat /var/lib/tor/honey/hostname`
root@ohdzjoric6qwtr2c.onion's password: 
Linux debian 2.6.32-5-amd64 #1 SMP Mon Feb 25 00:26:11 UTC 2013 x86_64

The programs included with the Debian GNU/Linux system are free software;
the exact distribution terms for each program are described in the
individual files in /usr/share/doc/*/copyright.

Debian GNU/Linux comes with ABSOLUTELY NO WARRANTY, to the extent
permitted by applicable law.
Last login: Fri May  3 20:10:22 2013 from localhost
root@debian:~# dd if=/dev/urandom of=data count=1k
1024+0 records in
1024+0 records out
524288 bytes (524 kB) copied, 0.081219 s, 6.5 MB/s
root@debian:~# md5sum data
81d52fca4cfe42dca24659850139672a  data
root@debian:~# logout # latency about 1-2 sec.
Connection to ohdzjoric6qwtr2c.onion closed.
root@debian:~# torsocks scp `cat /var/lib/tor/honey/hostname`:data copy
root@ohdzjoric6qwtr2c.onion's password: 
data                                          100%  512KB  28.4KB/s   00:18    
root@debian:~# md5sum copy
81d52fca4cfe42dca24659850139672a  copy
root@debian:~#

$ cat hex 
02000000
f40457b1
d005aeec
6e4fe577
f2a76dc3
73ef8901
220376b7
2b6de55a
00000000
bdcb52b0
9c48d2ee
26a513cb
cead7fb7
7daf4cef
9e2ab83b
bb9eb6b0
a7f5f990
fd270c51
378a0e1c
381353fa
$ xxd -r -p hex data
$ shasum -a 256 data >hash1
$ xxd -r -p hash1 bin
$ shasum -a 256 bin
e340423dffb20d7d21f17dfa272c527d84c20662061ce635627d0f0200000000  bin
$

IBM Journal of Research and Development, vol. 5, pp. 183-191 (1961)
Rolf Landauer

It is argued that computing machines inevitably involve devices which perform logical functions that do not have a single-valued inverse. This logical irreversibility is associated with physical irreversibility and requires a minimal heat generation, per machine cycle, typically of the order of kT for each irreversible function. This dissipation serves the purpose of standardizing signals and making them independent of their exact logical history. Two simple, but representative, models of bistable devices are subjected to a more detailed analysis of switching kinetics to yield the relationship between speed and energy dissipation, and to estimate the effects of errors induced by thermal fluctuations.

http://folk.uio.no/feder/Fys3130/Entropy/Landauer1961.pdf

See also discussion of Landauer's principle.

В монографии "Ламбда-исчисление. Его синтаксис и семантика", Барендрегт Х., 1985 (перевод с английского Г. Е. Минца под редакцией А. С. Кузичева), в параграфе 16.4 рассматривается эквациональная теория B = {M = N | M, N ∈ Λ₀, BT(M) = BT(N)}, где BT(M) - дерево Бема для терма M (см. "Краткое изложение λ-исчисления"). Иными словами, в этой теории отождествяются термы, имеющие одни и те же деревья Бема. Теория B непротиворечива, так как является собственным подмножеством ее экстенсионального расширения Bη, которое, в свою очередь, совпадает с единственной HP-полной λ-теорией H*.

Все комбинаторы неподвижной точки имеют одно и то же дерево Бема, поэтому они отождествляются в теории B. Более того, существуют термы, которые формально не подпадают под определение комбинаторов неподвижной точки, но имеют то же самое дерево Бема. Термы, которым соответствует дерево Бема комбинаторов неподвижной точки, обобщенно называются нестандартными комбинаторами неподвижной точки, а термы из этого множества, не являющиеся комбинаторами неподвижной точки, в свою очередь, называют существенно нестандартными. В следующей статье показывается, что множество нестандартных комбинаторов неподвижной точки не является рекурсивно перечислимым, в отличие от множества обычных комбинаторов неподвижной точки.

On the Recursive Enumerability of Fixed-Point Combinators
Mayer Goldberg

We show that the set of fixed-point combinators forms a recursively-enumerable subset of a larger set of terms we call non-standard fixed-point combinators. These terms are observationally equivalent to fixed-point combinators in any computable context, but the set of non-standard fixed-point combinators is not recursively enumerable.

http://www.brics.dk/RS/05/1/BRICS-RS-05-1.pdf

Operational equivalence for interaction nets
Maribel Fernández, Ian Mackie

The notion of contextual (or operational) equivalence is fundamental in the theory of programming languages. By setting up a notion of bisimilarity, and showing that it coincides with contextual equivalence, one obtains a simple coinductive proof technique for showing that two programs are equivalent in all contexts. In this paper we apply these (now standard) techniques to interactions nets, a graphical programming language characterized by local reduction. This work generalizes previous studies of operational equivalence in typed interaction nets since it can be applied to untyped systems, thus all systems of interaction nets are captured.

http://www.sciencedirect.com/science/article/pii/S0304397502006370

Observational Equivalence for the Interaction Combinators and Internal Separation
Damiano Mazza

We define an observational equivalence for Lafont's interaction combinators, which we prove to be the least discriminating non-trivial congruence on total nets (nets admitting a deadlock-free normal form) respecting reduction. More interestingly, this equivalence enjoys an internal separation property similar to that of Böhm's Theorem for the λ-calculus.

http://www.sciencedirect.com/science/article/pii/S1571066107001880

http://mathoverflow.net/questions/126941/

Существуют несколько способов представить λ-термы в сетях взаимодействия; например, алгоритм Лэмпинга для оптимальной редукции или компиляция λ-исчисления в комбинаторы взаимодействия. Однако, все известные нам способы реализуют только β-редукцию, но не экстенсиональное λ-исчисление (где также есть η-редукция).

Можно ли представить λ-термы в сетях взаимодействия, реализовав βη-редукцию?

(Нормальная форма сети для терма должна соответствовать его βη-нормальной форме.)

http://arxiv.org/abs/1304.1309

Interaction Nets in Russian

Draft translation to Russian of Chapter 7, Interaction-Based Models of Computation, from Models of Computation: An Introduction to Computability Theory by Maribel Fernandez. "In this chapter, we study interaction nets, a model of computation that can be seen as a representative of a class of models based on the notion of 'computation as interaction'. Interaction nets are a graphical model of computation devised by Yves Lafont in 1990 as a generalisation of the proof structures of linear logic. It can be seen as an abstract formalism, used to define algorithms and analyse their cost, or as a low-level language into which other programming languages can be compiled. This is fruitful because interaction nets can be implemented with reasonable efficiency."

Andrej Bauer
University of Ljubljana, Slovenia; Member, School of Mathematics
March 18, 2013 - 2:00pm

Discussions about constructive mathematics are usually derailed by philosophical opinions and meta-mathematics. But how does it actually feel to do constructive mathematics? A famous mathematician wrote that "taking the principle of excluded middle from the mathematician would be the same, say, as proscribing the telescope to the astronomer or to the boxer the use of his fists." Was he right? In this talk we shall visit the astounding worlds of constructive mathematics. As tourists from the classical world we will at first be shocked by the bizarre and unfamiliar phenomena, but hopefully also left curious about the new possibilities and dimensions of mathematics that the classical dogma declares heretical or even non-existent.

http://video.ias.edu/members/1213/0318-AndrejBauer

Я перевел на русский язык седьмую главу "Interaction-Based Models of Computation" из учебника "Models of Computation: An Introduction to Computability Theory" (Maribel Fernández). Исходник и PDF доступны на ShareLaTeX по следующему адресу:

https://www.sharelatex.com/project/515429c83d69291740451afe

В этой главе изучаются сети взаимодействия - модель вычислений, которую можно рассматривать как представителя класса моделей, основанных на идее "вычислений через взаимодействие". Сети взаимодействия являются графической моделью вычислений, изначально введенной как обобщение структур доказательств линейной логики. Данный формализм используется для описания алгоритмов и анализа их сложности, а также как язык низкого уровня, в который можно компилировать другие языки программирования. Особенно интересны сети взаимодействия тем, что они могут быть реализованы с разумной эффективностью.

Системы сетей взаимодействия определяются двумя множествами: набором агентов и набором правил взаимодействия. Агенты играют роль логических символов, а правила взаимодействия определяют их смысл. Также возможна аналогия с электрическими цепями, где агенты играют роль узлов цепи, а связи между агентами служат ветвями, соединяющими узлы. Наконец, мы можем просто считать агенты некоторыми объектами, выполняющими вычисления, при этом правила взаимодействия описывают их поведение.

Здесь дается общее представление о парадигме взаимодействия, приводятся примеры использования сетей взаимодействия для представления алгоритмов, а также показывается, как другие модели вычислений представляются в виде сетей взаимодействия.

http://arxiv.org/abs/1304.0558

This text gives a rough, but linear summary covering some key definitions, notations, and propositions from Lambda Calculus: Its Syntax and Semantics, the classical monograph by Barendregt. First, we define a theory of untyped extensional lambda calculus. Then, some syntactic sugar, a system of combinatory logic, and the fixed point theorem are described. The final section introduces a topology on the set of lambda terms which is meant to explain an illusory contradiction. Namely, functions defined on the set of lambda terms are in the set of lambda terms itself, the latter being a countable set. However, the functions on the set of lambda terms appear to be continuous with respect to a topology of trees.

На ShareLaTeX теперь доступно краткое изложение λ-исчисления:

https://www.sharelatex.com/project/5154436b3d6929174048f846

Данный текст представляет собой чрезвычайно сжатый конспект классической монографии по λ-исчислению (Х. Барендрегт, «Ламбда-исчисление. Его синтаксис и семантика», перевод с английского Г. Е. Минца под редакцией А. С. Кузичева, Москва, «Мир», 1985).

Он может оказаться интересен всем тем, кто планировал взяться за систематическое изучение данной темы, уже в общих чертах ознакомившись с ней, но откладывал из-за сложной структуры основной монографии, определения и основные результаты в которой довольно разрозненны. Здесь мы попытаемся сделать изложение, напротив, абсолютно линейным, и, конечно, несравнимо более коротким, избегая лишних определений и примеров, а сосредоточившись на необходимых терминологии, обозначениях и утверждениях, которые, в свою очередь, изложены близко к оригинальному тексту.

Мы начнем от определения системы λβη, то есть классического бестипового экстенсионального λ-исчисления. Затем перейдем к комбинаторной логике, теореме о неподвижной точке и синтаксическому сахару. Наконец, заключительная часть конспекта — построение топологии на выражениях этой системы, призванной объяснить кажущееся противоречие: отображения множества выражений в себя содержатся в самом этом множестве при его счетности. На самом же деле, множество наделяется надлежащей топологией, в которой выражения представляют собой непрерывные отображения.

Кстати, сервис ShareLaTeX оказался чрезвычайно удобным. Горячо рекомендую его для хранения математических текстов и, в том числе совместного, их редактирования. Собираюсь использовать его для перевода седьмой главы о системах взаимодействия прекрасного учебника по моделям вычислений. Скорее всего, перевод будет доступен по следующему адресу:

https://www.sharelatex.com/project/515429c83d69291740451afe

Всячески рекомендую всем замечательный учебник Maribel Fernandez под названием "Models of Computation: An Introduction to Computability Theory". С одной стороны, он написан сжато и по существу, но при этом простым языком, содержит упражнения и покрывает современный материал.

Учебник начинается с введения в классическую теории вычислимости: машины Тьюринга и лямбда-исчисление. Затем следует подробное описание систем взаимодействия, включая полезную нотацию Lafont. Наконец, дается обзор некоторых зарождающихся направлений.

A Concise Introduction to Computation Models and Computability Theory provides an introduction to the essential concepts in computability, using several models of computation, from the standard Turing Machines and Recursive Functions, to the modern computation models inspired by quantum physics. An in-depth analysis of the basic concepts underlying each model of computation is provided. Divided into two parts, the first highlights the traditional computation models used in the first studies on computability:

- Automata and Turing Machines;
- Recursive functions and the Lambda-Calculus;
- Logic-based computation models.

The second part covers object-oriented and interaction-based models. There is also a chapter on concurrency, and a final chapter on emergent computation models inspired by quantum mechanics. At the end of each chapter there is a discussion on the use of computation models in the design of programming languages.

http://www.amazon.co.uk/dp/1848824335

Lähetämme Teille ohessa uuden ajokorttinne numero 2013XXXXXXXXXX, joka on voimassa 19.01.2013-19.01.2028. Pyydämme teitä tarkistamaan, että ajokortilla olevat tiedot ovat oikein.

Jos Teillä on aiempi ajokortti, sen voimassaolo on päättynyt. Aiempi ajokortti on palautettava oheisessa palautuskuoressa. Postimaksu on maksettu. Jos aiempi ajokorttinne on kadonnut tai anastettu, Teidän on tehtävä anastus- tai katoamisilmoitus poliisille. Jos olette jo tehnyt ilmoituksen, asia on kunnossa.

Jos olette ajokiellossa, tämän ajokortin vastaanottaminen ei palauta ajo-oikeutta. Teidän on palautettava nyt vastaanottamanne ajokortti poliisille.

Мы уже затрагивали переход от условного выражения к функциям-проекциям для конечных последовательностей, когда обсуждали логические операции без сравнений. Однако, теперь мы можем обобщить также условное выражение, реализованное с помощью одной примитивной операции, а не двух, как раньше. Мы будем опираться на определения и обозначения, введенные при рассмотрении GRS из одной примитивной операции.

Благодаря незамысловатому разделению памяти, для представления всех функций-проекций для последовательностей длиной n или менее элементов, нам потребуется ровно n нод: